I previously written about understanding what Merkle trees are. If you haven’t read it, go and do so now.
I tried to keep it non-technical, and a keen observer would point out that the article better explained the benefits of hashing rather than of Merkle trees. I was trying to explain why Bitcoin benefited from Merkle trees, rather than how they actually worked.
In my previous article, the gist was that hashing allows you to verify that large quantities of data haven’t been changed using a hash, a much smaller amount of data. Merkle trees basically allow you to verify that a particular piece of data was present and hasn’t been manipulated, using only a small number of proofs rather than having to download all the data to check for yourself.
This time, I’m going to have another go at explaining Merkle trees, with the assistance of something we can all relate to… colours. I’m going to create what I’ve called a Merkcolour tree (see what I did there).
A Bitcoin transaction hash is the unique identifier for each transaction. In a block there are is as much as 1MB worth of transaction data. You can hash all the transactions in a block into a single 256-bit hash. However in order to prove that a transaction existed in a block you would have to download all the data used to create the hash, generate your own hash to check it is accurate, and then check transaction you wanted to verify was present in the data.
This would make it possible to store a copy of the 256-bit block hashes without having to store all the transaction data (upto 1MB) for each block – the down side is that in order to check a transaction is present you have to download all the transactions data instead of a small number of proofs, which is much more quicker and efficient as Merkle trees enable.
So how do Merkle trees work?
Well, the unique Bitcoin transaction id, which is actually a hash created by hashing the transaction information together, looks like this:
cf92a7990dbae2a503184d6926be77fc85e9a9275f4222064ee78eeb251d36b2
And if you combine (concatenate) two transaction ids back to back:
cf92a7990dbae2a503184d6926be77fc85e9a9275f4222064ee78eeb2 51d36b2d8f4744017dc79f8df24e2dba7fd28e5fd148c3b01b5f76dede8ef3ac4e5c340
That combined data can be hashed together (using the SHA-256 method) into the following hash:
474a1d00a80dd927ba87404371c11c7db24bc58b0a712ffacdb09a47dc1bec89
Instead 512-bits of data for both transactions, the hash is 256-bits of data.
Now lets adapt this logic to colours. Each colour is represented in the same hexadecimal format as a hash, it’s just that a 256-bit hash is more than 10 times longer than a 24-bit colour.
As an example, red is #ff0000, blue is #0000ff.
If we combine those colours together we get #800080.
Instead of 48-bits of data for both colours, the combined colour is 24-bits of data.
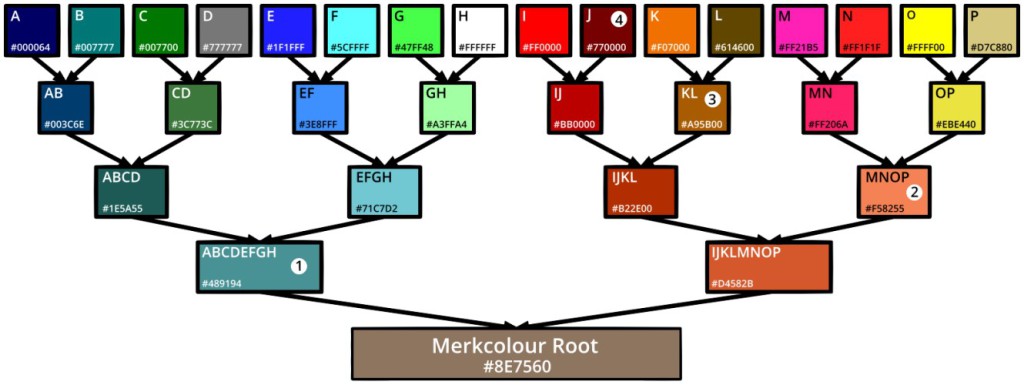
A Merkle tree is basically a process by which pairs of hashes are merged together, until you end up with just one, the root. This is best demonstrated with colours in the image below (click it to open).
In the image, we start with 16 different colours (labelled A to P) – these are the leaves. Each colour has been paired with a neighbour and combined together to create a branch. This process is repeated as many times as necessary until you end up with one final colour – the root.
Now, the colour (leaf) we’ve labelled I in the diagram is #ff0000.
If, instead of creating a tree, I simply hashed all the colours together the outcome would be as follows:
#000064#007777#007700#777777 #1f1fff#5cffff#47ff48#ffffff #ff0000#770000#f07000#614600 #ff21b5#ff1f1f#ffff00#d7c880
Hashes (using the MD5 method) to:
8c4878686b62656fbe81d50c3a832728
If I provided you with that hash, and told you it included the colour #ff0000, the only way I can prove it is by sending you all 16 colours in that order (384-bits of data, removing the #) so you can generate and confirm the accuracy of the hash for yourself.
However, because we’ve created a tree, if you know the root is #8e7560 (a product of all leaves – ABCDEFGHIJKLMNOP), we can confirm that #ff0000 (I) was included using only 4 proofs:
- #489194 (ABCDEFGH)
- #f58255 (MNOP)
- #a95b00 (KL)
- #770000 (J)
Let’s start at the top and work our way down to the root:
#ff0000 (I) (we want to confirm) when combined with 4) #770000 (J) gives:
#bb0000 (IJ) which combined with 3) #a95b00 (KL) gives:
#b22e00 (IJKL) which combined with 2) #f58255 (MNOP) gives:
#d4582b (IJKLMNOP) which combined with 1) #489194 (ABCDEFGH) gives:
#8e7560 – which is the correct root!
If we ended up with any other value than the root, we know some of the data we have been given is inaccurate and cannot be trusted.
This means that instead of hashing all the colours together and needing to download 384-bits of data to confirm its accuracy, we are able to download just 4 proofs, or 96-bits of data.
The efficiency gets even bigger the more leaves you have, as each time you double the data (number of leaves), you only add one additional branch which is one extra 24-bit proof for colours, or 256-bit proof for hashes.
For example here’s how much proof data is required to verify the following:
32 colours (768-bits): 5-proofs (120-bits, 84% efficiency)
64 colours (1536-bits): 6-proofs (144-bits, 91% efficiency)
128 colours (3072-bits): 7-proofs (168-bits, 95% efficiency)
256 colours (6144-bits): 8-proofs (192-bits, 97% efficiency)
512 colours (12288-bits): 9-proofs (216-bits, 98% efficiency)
1024 colours (24576-bits): 10-proofs (240-bits, 99% efficiency)
A key distinction of hashes and colours is that hashes are one-way and unpredictable. That means you cannot work out what two hashes were combined to create a hash. The opposite is true for colours, if you know a colour it is possible to work out exactly what combinations of colours could have created it. The Merkcolour tree is only useful for visually demonstrating the concept, if you could reverse engineer a hash in the same way you can a colour it would not be reliable.
Hopefully this makes sense! The key take home message is that instead of having to download an entire 1MB block to confirm that a transaction was in it, you’re able to download a small number of proofs for validation. This makes it a lot easier to verify transactions without having to keep a copy of the blockchain or download large quantities of data, for example on devices such as smartphones where this is less practical.
Merkle trees make the process of verifying data hugely efficient, and while Bitcoin could exist without them, it would require an awful lot more resources such as processing, bandwidth and storage – and running clients on mobile devices would be far less viable.
Thank you Ralph Merkle.
John Hardy
Email [email protected]
Latest posts by John Hardy (see all)
- The great P2PK Bitcoin heist. Millions of Bitcoins WILL be stolen, but should we even try to stop it? - 24 Aug 2018
- Follow up: Bitcoin Cash has 51% attack vulnerability double jeopardy - 31 Jul 2018
- Bitcoin rival has a major vulnerability which could help Bitcoin miners to destroy it in 2020 - 30 Jul 2018

Just pure awesomeness ! I read many articles,but none could beat this as you ultimately nailed it to the level it needs to for actually someone to know the damn benefit of these trees.